元素周期表

我们不妨先根据构造原理写出每一能层的电子数：

$1 \text s$	$2 \text s$|$2 \text p$	$3 \text s$|$3 \text p$	$4 \text s$|$3 \text d$|$4 \text p$	$5 \text s$|$4 \text d$|$5 \text p$	$\cdots$
$2$	$2$|$6$	$2$|$6$	$2$|$10$|$6$	$\cdots$	$\cdots$
$2$	$4$|$10$	$12$|$18$	$20$|$30$|$36$	$54$	$\cdots$
$\text{He}$	$\text{Ne}$	$\text{Ar}$	$\text{Kr}$	$\text{Xe}$	$\text{Rn}$

根据这些可得到元素周期表的雏形：

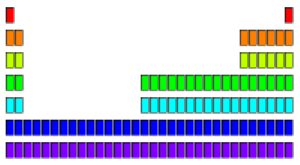
因此我们可以归纳出下列的规律：

• 第 $n$ 周期从 $n \text s^1$ 开始，到 $n \text p^6$ 结束（除第一周期外）。
• 同周期元素红出现的电子排布轨道能量接近，可以称为一个能级组。

---

思考

1. 列出第 $n$ 周期的能级组

解：第一周期的能级组有 $1 \text s$，第二周期有 $2 \text s$ 和 $2 \text p$。依此类推，可以得到一般规律（该能级组包含对应能级的前提是该能级存在）：

$$n \text s,\cdots,(n-2) \text f,(n-1) \text d,n \text p$$

2. 第十周期有多少个原子？

解法一：第 $n$ 周期有 $2 \lceil \frac{n+1}{2} \rceil^2$ 个原子。将 $n=10$ 代入得共有 $2 \times 6^2=72$ 个原子。

解法二：根据第 $1$ 题的启发，可以先列出第十周期的能级组。

先列好两端的 $\text s$ 和 $\text p$：

$$10 \text s,10 \text p$$

再依次添加剩余的轨道：

$$10 \text s,{\color{green}{9 \text d}},10 \text p$$

$$10 \text s,{\color{green}{8 \text f}},9 \text d,10 \text p$$

$$10 \text s,{\color{green}{7 \text g}},8 \text f,9 \text d,10 \text p$$

$$10 \text s,{\color{green}{6 \text h}},7 \text g,8 \text f,9 \text d,10 \text p$$

$$10 \text s,{\color{red}{5 \text i}},6 \text h,7 \text g,8 \text f,9 \text d,10 \text p$$

注意到 $5 \text i$ 并不存在，因此能级组为：

$$10 \text s,6 \text h,7 \text g,8 \text f,9 \text d,10 \text p$$

进行累加，可得最多可容纳的电子数为

$$2+6+10+14+18+22=\frac{(2+22) \times 6}{2}=72$$

因此第十周期有 $72$ 个原子。

---