能级交错
在电子需要进入原子轨道时,按照一定的规律进行填入:
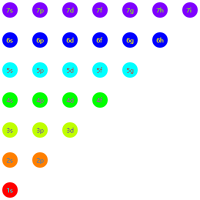
可以想象有一个与坐标轴正半轴夹角为 $135^\circ$ 的直线,每次先从右下到左上读出所有元素,然后右移动 $1$ 格,重复操作即可得到所有排布的顺序:
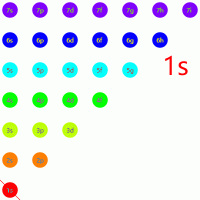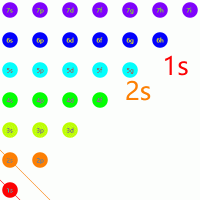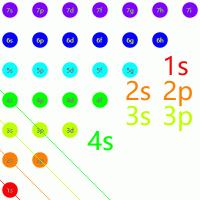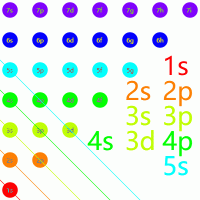
练习
- $\text{Fe}$ 原子的电子排布
解:$\text{Fe}$ 为 $26$ 号元素,因此有 $26$ 个核外电子。不妨先把前面的轨道列出:
$$1 \text s,2 \text s,2 \text p,3 \text s,3 \text p,4 \text s,3 \text d,4 \text p,5 \text s$$
前六个轨道可容纳 $2(1+1+3+1+3+1)=20$ 个电子,而最后 $6$ 个电子可以直接排列在下一个轨道 $3 \text d$ 中($6 \ge 10$)。
因而电子排布为
$$1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6 4 \text s^2 3 \text d^6$$
- $\text{Br}$ 原子的电子排布
解:$\text{Br}$ 为 $35$ 号元素,因此有 $35$ 个核外电子。因而电子排布为
$$1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6 4 \text s^2 3 \text d^{10} 4 \text p^5$$
注意到我们可以列出稀有气体的电子排布式(按照轨道顺序排列):
$\text{He}$ $1 \text s^2$
$\text{Ne}$ $1 \text s^2 2 \text s^2 2 \text p^6$
$\text{Ar}$ $1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6$
$\text{Kr}$ $1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6 3 \text d^{10} 4 \text s^2 4 \text p^6$
$\text{Xe}$ $1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6 3 \text d^{10} 4 \text s^2 4 \text p^6 4 \text d^{10} 5 \text s^2 5 \text p^6$
这些稀有气体除了 $\text{He}$ 以外,都以 $n \text p^6$ 结尾,因此可以用来简化电子的排布:
$\text{Fe}$ $1 \text s^2 2 \text s^2 2 \text p^6 3 \text s^2 3 \text p^6 4 \text s^2 3 \text d^6 \to [\text{Ar}]3 \text d^6 4 \text s^2$
对于阳离子,应当先写出对应离子的排布,再按从外到内的顺序进行丢失:
$\text{Fe}$ $[\text{Ar}]3 \text d^6 4 \text s^2 \to \text{Fe}^{3+}$ $[\text{Ar}]3 \text d^5$
洪特规则补充条例
在能量相同的轨道中电子全部充满、半充满和全空时相对较稳定。
因此需要补充下面两个特例:
$_{24}\text{Cr}$ 按之前为 $[\text{Ar}]3 \text d^4 4 \text s^2$,但实为 $[\text{Ar}]3 \text d^5 4 \text s^1$。
$_{29}\text{Cu}$ 按之前为 $[\text{Ar}]3 \text d^9 4 \text s^2$,但实为 $[\text{Ar}]3 \text d^{10} 4 \text s^1$。