原子的构造原理 题解

练习 1

A. 和电子层相关联的是能层而不是能级，A 错误。

B. 每个能层有轨道 $0 \sim n-1$，因此可容纳的总电子数为 $2 \sum_{i=0}^{n-1} (2i+1)=2(n^2-n+n)=2n^2$，B 正确。

C. 在不考虑能级交错的情况下，不同能层按能层从小到大的顺序能量从低到高，相同能层按能级从小到大的顺序能量从低到高。而能级交错只是对部分能级的交换，但本身能量没有改变，因此同一能层的不同能级能量不可能相同。C 错误。

D. 与 C 类似，能层不同时层数越大，能量越大。D 错误。

练习 2

$\text O$ 的电子排布为 $1 \text s^2 2 \text s^2 2 \text p^4$。形成阴离子时可直接追加电子，因此 $\text O^{2-}$ 的电子排布为 $1 \text s^2 2 \text s^2 2 \text p^6$，故 B 错误。

练习 3

最外层电子排布可以反映最外层电子数，从而体现元素的化合价。而 $\text X_2 \text Y_3$ 这一形式也表明 $\text X$ 化合价为正，$\text Y$ 为负。

A. $\text X$ 和 $\text Y$ 的最外层电子数分别为 $2+1=3$ 和 $2+5=7$。因此 $\text X,\text Y$ 化合价分别为 $+3,-1$，不合题意。

B. $\text X$ 和 $\text Y$ 的最外层电子数分别为 $2+3=5$ 和 $2+4=6$。因此 $\text X,\text Y$ 化合价分别为 $+5,-2$，不合题意。

C. $\text X$ 和 $\text Y$ 的最外层电子数分别为 $2+1=3$ 和 $2+4=6$。因此 $\text X,\text Y$ 化合价分别为 $+3,-2$，符合题意。

D. $\text X$ 和 $\text Y$ 的最外层电子数分别为 $2$ 和 $2+3=5$。因此 $\text X,\text Y$ 化合价分别为 $+2,-3$，不合题意。

练习 4

C 中 $2 \text p$ 没有排满，而该元素又不是 $\text{Cr}$ 和 $\text{Cu}$ 的特例，因此 C 不符合题意。

练习 5

$3 \text d$ 轨道上排满后应该有 $6$ 个电子，而现在只有 $5$ 个电子。因此只可能有两种情况：

• 某一元素排到 $3 \text d$ 前只差 $5$ 个电子就可以排完。因此该元素电子数为 $2+2+6+2+6+2+5=25$，即为 $_{25}\text{Mn}$。
• 该元素符合洪特规则补充条例，即为 $_{24}\text{Cr}$。

$\text{Mn}$ 和 $\text{Cr}$ 的排布式分别为 $3 \text d^5 4 \text s^2$ 和 $3 \text s^2 3 \text p^6 3 \text d^5$，因此 D 符合题意。

练习 6

A. 同一名称的能级所含轨道数相同，差别只在于能量大小，A 错误。

B. 这一过程部分电子从外侧转移到内侧，因此释放能量，B 正确。

C. $3 \text p^2$ 表示 $3 \text p$ 能级上有两个电子，C 错误。

D. 不可能存在两个主量子数、角量子数、磁量子数和自旋量子数都对应相等的电子。因此不可能存在运动状态相同的电子，D 错误。

任务

当不考虑能级交错时，这一世界的排布规律如下：

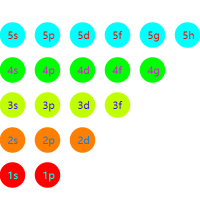
注意到磁量子数为 $\pm l$，因此只有当角量子数为 $0$ 时每个轨道可容纳 $1$ 个电子，其它情况均可容纳 $2$ 个电子。

题目询问的是第三个稀有气体，因此该元素应该正好排满了前三能层的所有轨道。

因此电子数为 $1+2+1+2+2+1+2+2+2=15$，即对应第 $15$ 号元素。