P7806 「DCOI2021」A 冰魄吐息 题解

题目中出现了至多和最小等字眼，因此很有可能需要使用二分答案。

怎么进行二分呢？我们对 $d$ 进行二分并检验当前 $d$ 值是否符合题意。不难发现，如果一个点到原点的距离不超过 $d$，那么这个点一定符合（所有正比例函数都经过原点）。因此我们只需考虑 $x^2+y^2 \gt d^2$ 的点。

由于到一个点距离不超过 $d$ 的集合就是以该点为圆心，$d$ 为半径的圆内，因此我们只需要求出该圆过原点的两条切线的斜率即可。显然在这两条直线 $y=Lx$ 和 $y=Rx$ 之间（不一定是斜率之间）的所有直线都是符合题意的：

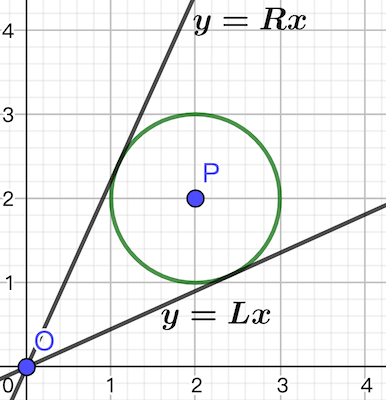
我们只需要找到这 $n$ 个点对应的 $L,R$ 值，将这些点的 $[L,R]$ 抽象成 $n$ 条线段，就可以把问题转化成用最少的点覆盖所有线段的经典贪心问题，并以最少的点数是否小于等于 $k$ 作为二分答案的判断条件。

那么最关键的就是如何求解每个点的 $L,R$。这里有三种方法：

Solution 1 二分套二分

为什么题目要提供点和直线的距离公式呢？实际上，根据之前插图的演示，不难发现直线与点的距离满足一定的单调性。我们可以利用这个性质再一次二分，得到 $L,R$ 的值。

对于斜率等于 $+\infty$ 的情形，我们可以直接在二分前进行处理，例如将其修改成一个足够大的数。

该做法的时间复杂度为 $\mathcal O(n \log x \log x+n \log n \log x)$（$x$ 为二分区间大小）：

#include<bits/stdc++.h>
using namespace std;
int n,k;
long double l,r=100000,ans; // 将二分区间右端点 r 调成一个较大的值
struct point
{
    long double x,y;
}p[25001];
struct interval
{
    long double L,R;
    bool operator<(const interval &x)const
    {
        return R<x.R;
    }
}a[25001];
bool check_dis(int x,int y,long double k,long double d)
{
    long double dis=fabs(y-k*x)/sqrt(k*k+1);
    return dis<=d;
}
interval get(point p,long double d)
{
    if(!p.x)return (interval){-p.y/d,p.y/d}; // 特判 x 为 0 的特例
    interval ans;
    long double l=0,r=p.y/p.x; // 第一条切线一定在点 P 的下方
    while(l<=r)
    {
        long double mid=(l+r)*0.5;
        if(check_dis(p.x,p.y,mid,d))
        {
            r=mid-0.00000001; // 第二个二分需要很高的精度，否则无法通过
            ans.L=mid;
        }
        else l=mid+0.00000001;
    }
    l=p.y/p.x,r=100000; // 第二条切线一定在点 P 的上方
    while(l<=r)
    {
        long double mid=(l+r)*0.5;
        if(check_dis(p.x,p.y,mid,d))
        {
            l=mid+0.00000001;
            ans.R=mid;
        }
        else r=mid-0.00000001;
    }
    return ans;
}
bool check(long double d)
{
    int cnt=0;
    for(int i=1;i<=n;++i)
    {
        if(sqrt(p[i].x*p[i].x+p[i].y*p[i].y)<=d)continue; // 不需要考虑到原点距离已经不超过 d 的点
        a[++cnt]=get(p[i],d); // 二分得到斜率区间
    }
    sort(a+1,a+cnt+1); // 排序并用贪心求解
    int tot=0;
    long double tmp=0;
    for(int i=1;i<=cnt;++i)
    {
        if(tmp<=a[i].L)
        {
            tmp=a[i].R;
            if(++tot>k)return false; // 一旦需要的直线数量超过 k 就说明不可行
        }
    }
    return true;
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y);
    while(l<=r)
    {
        long double mid=(l+r)*0.5;
        if(check(mid))
        {
            r=mid-0.0001; // 由于只需要保留两位小数，因此精度可以稍低
            ans=mid;
        }
        else l=mid+0.0001;
    }
    printf("%.2Lf",ans);
    return 0;
}

Solution 2 二分+导角

我们可以通过角和斜率之间的转化求解。

考虑下图的情形（两条直线斜率都非负）：

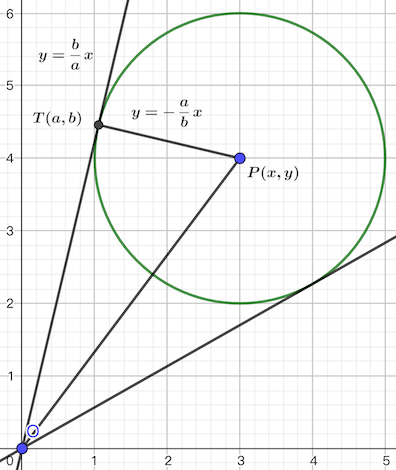
我们可以用反正切函数求出 $PO$ 与 $x$ 轴正方向的夹角 $\alpha$，用反正弦函数求出 $\beta=\angle TOP$。由于两条切线与 $OP$ 之间的夹角相等，因此两条切线与 $x$ 轴正半轴的夹角为 $\alpha ± \beta$。

我们还需考虑下面两种情形：

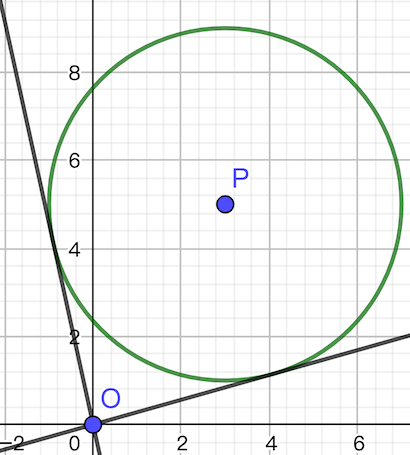
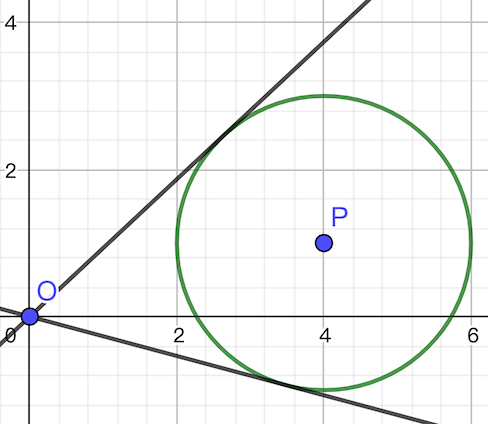
这种情形下切线斜率一正一负，而这此时直接把负的当左端点、正的当右端点显然是错误的（有一个跨 $0$ 的过程）。又因为题中没有负坐标，因此只需要保留正斜率。那么：

• 在第一种情形中，符合题意的所有斜率的最小值为其中的正斜率，最大值为 $+\infty$。
• 在第二种情形中，最小值为 $0$，最大值为其中的正斜率。

考虑当前的点属于哪一种情形：

• 当切点位于第二象限时（此时 $\alpha+\beta \gt 90^\circ$），属于第一种。
• 当切点位于第四象限时（此时 $\alpha+\beta \lt 90^\circ$），属于第二种。

那么，为什么二分套二分的方法不需要对此进行考虑呢？这是因为，我们可以在求解 $L,R$ 时将二分下界设为 $0$，这样就避免了需要讨论负斜率的情况。

该做法的时间复杂度为 $\mathcal O(n \log x+n \log n)$：

#include<bits/stdc++.h>
using namespace std;
const double rt=acos(-1)*0.5; // 预处理 90° 弧度制下的值，即 0.5π
int n,k;
long double l,r=100000,ans;
struct point
{
    long double x,y;
}p[25001];
struct interval
{
    long double L,R;
    bool operator<(const interval &x)const
    {
        return R<x.R;
    }
}a[25001];
bool check(long double d)
{
    int cnt=0;
    for(int i=1;i<=n;++i)
    {
        long double x=p[i].x,y=p[i].y;
        if(x*x+y*y<=d*d)continue;
        ++cnt;
        long double alpha,beta;
        alpha=atan(y/x); // 求出 OP 与 x 轴的夹角
        if(!x)alpha=rt; // 如果 x=0 则与 x 轴的夹角为 90°
        beta=asin(d/sqrt(x*x+y*y)); // 求出切线与 OP 连线的夹角
        a[cnt].L=tan(alpha-beta),a[cnt].R=tan(alpha+beta);
        if(a[cnt].L>a[cnt].R)swap(a[cnt].L,a[cnt].R);
        if(a[cnt].L<0)
        {
            if(alpha+beta>rt)
            {
                a[cnt].L=a[cnt].R;
                a[cnt].R=1e18;
            }
            else a[cnt].L=0;
        }
    }
    sort(a+1,a+cnt+1);
    int tot=0;
    long double tmp=0;
    for(int i=1;i<=cnt;++i)
    {
        if(tmp<=a[i].L)
        {
            tmp=a[i].R;
            if(++tot>k)return false;
        }
    }
    return true;
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y);
    while(l<=r)
    {
        long double mid=(l+r)*0.5;
        if(check(mid))
        {
            r=mid-0.0001;
            ans=mid;
        }
        else l=mid+0.0001;
    }
    printf("%.2Lf",ans);
    return 0;
}

Solution 3 二分+导边

借助之前的示意图：

不妨设 $T$ 的坐标为 $(a,b)$，则 $OT$ 的斜率为 $\dfrac{b}{a}$，$TP$ 的斜率为 $-\dfrac{a}{b}$。把 $P(x,y)$ 和 $T(a,b)$ 代入得 $\dfrac{b-y}{a-x}=-\dfrac{a}{b}$。化简得 $a^2+b^2=ax+by$。

又因为 $TP=d$，因此有 $(x-a)^2+(y-b)^2=d^2$。化简得 $a^2+b^2-2ax-2by=d^2-x^2-y^2$。

由于 $x,y,d$ 为常数，因此可设 $c=d^2-x^2-y^2$。

因此

$$\begin{cases} a^2+b^2=ax+by & (1) \cr a^2+b^2-2ax-2by=c & (2) \cr \end{cases}$$

把 $(1)$ 代入 $(2)$ 得

$$ax+by=-c$$

因此我们可以将 $b$ 用 $a$ 进行表示（仅在 $y \neq 0$ 时成立）：

$$b=\dfrac{-c-ax}{y}$$

再代回 $(1)$ 得：

$$a^2+\dfrac{(c+ax)^2}{y^2}=-c$$

$$a^2y^2+c^2+2acx+a^2x^2+cy^2=0$$

$$(x^2+y^2)a^2+2cxa+c^2+cy^2=0$$

$$a_{1,2}=\dfrac{-2cx±\sqrt{4c^2x^2-4(x^2+y^2)(c^2+cy^2)}}{2(x^2+y^2)}$$

$$=\dfrac{-cx±\sqrt{c^2x^2-(x^2+y^2)(c^2+cy^2)}}{x^2+y^2}$$

$$=\dfrac{-cx±\sqrt{-cx^2y^2-y^2c^2-cy^4}}{x^2+y^2}$$

$$=\dfrac{-cx±y\sqrt{-c(x^2+y^2+c)}}{x^2+y^2}$$

最后求出 $b_{1,2}$ 即可得到两条直线的斜率。

特判 $y=0$ 的情形：

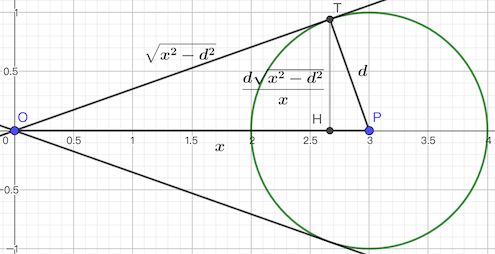
此时 $OP=x$，$TP=d$，$OT=\sqrt{x^2-d^2}$。

作 $TH \perp OP$ 于 $H$，则 $\sin \angle TOH=\dfrac{TP}{OP}=\dfrac{TH}{OT}$。因此 $\dfrac{d}{x}=\dfrac{TH}{\sqrt{x^2-d^2}}$，即 $TH=\dfrac{d\sqrt{x^2-d^2}}{x}$。然后再在 $\triangle OTH$ 中用一次勾股定理即可求出 $OH$。最后斜率即为 $\dfrac{TH}{OH}$。

由于 $y=0$，因此较下方的切线的斜率必然为负。之前提到了本题无需考虑负斜率，因此取斜率的最小值为 $0$，最大值为 $\dfrac{TH}{OH}$ 即可。

$x=0$ 的情形不需单独考虑，因为其斜率的范围显然为 $[-\dfrac{y}{d},\dfrac{y}{d}]$，适用于一般情况。

---

与导角的方法类似，我们仍需考虑这两种情形：

考虑每个点属于哪一种情形：

• 当负斜率的切点位于 $y$ 轴上方时，第一种情形成立。
• 当负斜率的切点位于 $y$ 轴下方时，第二种情形成立。

相比于导角的做法，该做法时间复杂度仍为 $\mathcal O(n \log x+n \log n)$，但不涉及反三角函数的使用，因此常数较小：

#include<bits/stdc++.h>
using namespace std;
int n,k;
long double l,r=100000,ans;
struct point
{
    long double x,y;
}p[25001];
struct interval
{
    long double L,R;
    bool operator<(const interval &x)const
    {
        return R<x.R;
    }
}a[25001];
bool check(long double d)
{
    int cnt=0;
    for(int i=1;i<=n;++i)
    {
        long double x=p[i].x,y=p[i].y;
        if(x*x+y*y<=d*d)continue;
        ++cnt;
        if(!y) // 考虑 y=0 的情况
        {
            a[cnt].L=0;
            long double b1=d*sqrt(x*x-d*d)/x;
            long double a1=sqrt(x*x-d*d-b1*b1);
            a[cnt].R=b1/a1;
        }
        else
        {
            long double c=d*d-x*x-y*y,delta=-c*(x*x+y*y+c);
            long double a1=(-c*x+y*sqrt(delta))/(x*x+y*y);
            long double a2=(-c*x-y*sqrt(delta))/(x*x+y*y);
            long double b1=(-c-a1*x)/y,b2=(-c-a2*x)/y;
            a[cnt].L=b1/a1,a[cnt].R=b2/a2;
            if(a[cnt].L>a[cnt].R)
            {
                swap(a[cnt].L,a[cnt].R);
                swap(a1,a2);
                swap(b1,b2);
                // 一定要注意连同 a1,a2,b1,b2 同时 swap，否则会影响下面对答案的修正
            }
            if(a[cnt].L<0) // 一正一负的情形下，负的必然存储在 L 中
            {
                if(b1>0)
                {
                    a[cnt].L=a[cnt].R;
                    a[cnt].R=1e18; // 将右端点赋为极大值
                }
                else a[cnt].L=0; // 否则将左端点由负改为 0 即可
            }
        }
    }
    sort(a+1,a+cnt+1);
    int tot=0;
    long double tmp=0;
    for(int i=1;i<=cnt;++i)
    {
        if(tmp<=a[i].L)
        {
            tmp=a[i].R;
            if(++tot>k)return false;
        }
    }
    return true;
}
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y);
    while(l<=r)
    {
        long double mid=(l+r)*0.5;
        if(check(mid))
        {
            r=mid-0.0001;
            ans=mid;
        }
        else l=mid+0.0001;
    }
    printf("%.2Lf",ans);
    return 0;
}