荆轲刺秦王 题解

本题的核心思想为 $\color{red}{\text{BFS}+差分}$。

$30$ 分算法

先输入矩阵。对于士兵，进行一个 $\mathcal O(nm)$ 的外层循环寻找士兵，再进行一个 $\mathcal O(nm)$ 的内层循环，标记士兵范围。以下为内层循环的函数：

void find(int x,int y,int z)
{
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            if(abs(i-x)+abs(j-y)<z)
                newmap[i][j]="#"; // 标记为 # 就表示该处为士兵可观测范围，士兵本身用 / 标记
}

维护一个队列并不断拓展，会有以下四种情况：

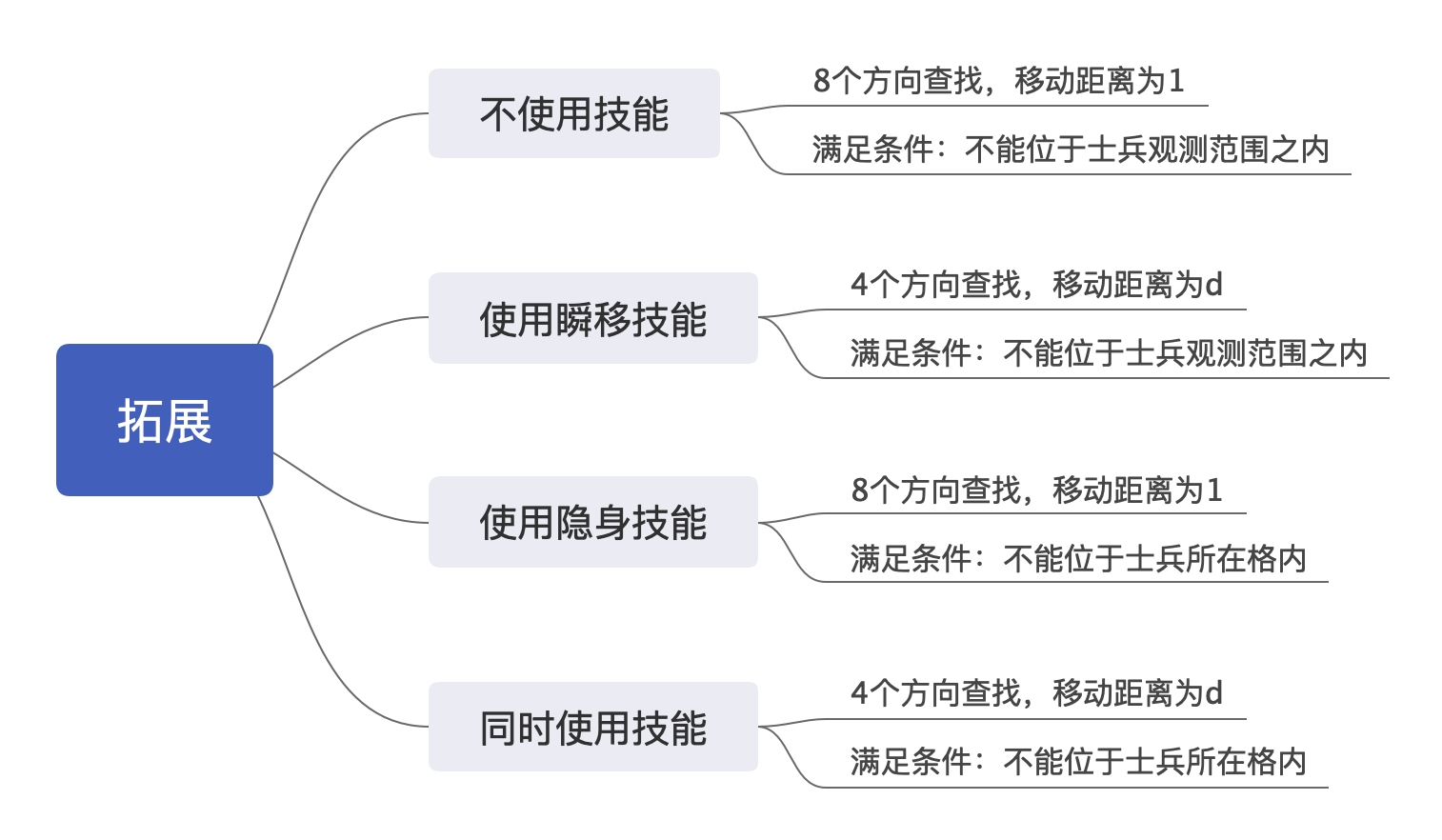
事实上，上述的优先级是从上到下的——不使用技能是最好的，其次是瞬移、隐身和同时使用：

在所用时间相同情况下，荆轲希望使用的两种技能总次数尽可能少；在所用时间与技能次数相同情况下，荆轲希望使用的隐身次数尽可能少。

按照这个顺序，我们一一进行拓展即可，最终只要到了秦王所在的格子就输出结果。
该算法其实是存在很多问题的，因为最优结果不一定是最先找到的，所以这样会导致 WA。而 RE 可能是因为数组元素量不够大导致的。TLE 则可能是由于多种因素导致的，我们要逐个解决。

$95$ 分算法

本算法需要改进的地方：

• 考虑最优情况，而不是最先遍历的情况

• 尽量减少程序运行的时间，进行有必要的剪枝

输入不提。我们可以考虑在士兵控制范围方面做一些改进，之前的内层循环是从 $1$ 到 $n$ ，从 $1$ 到 $m$ 的，但其实这都是不必要的。

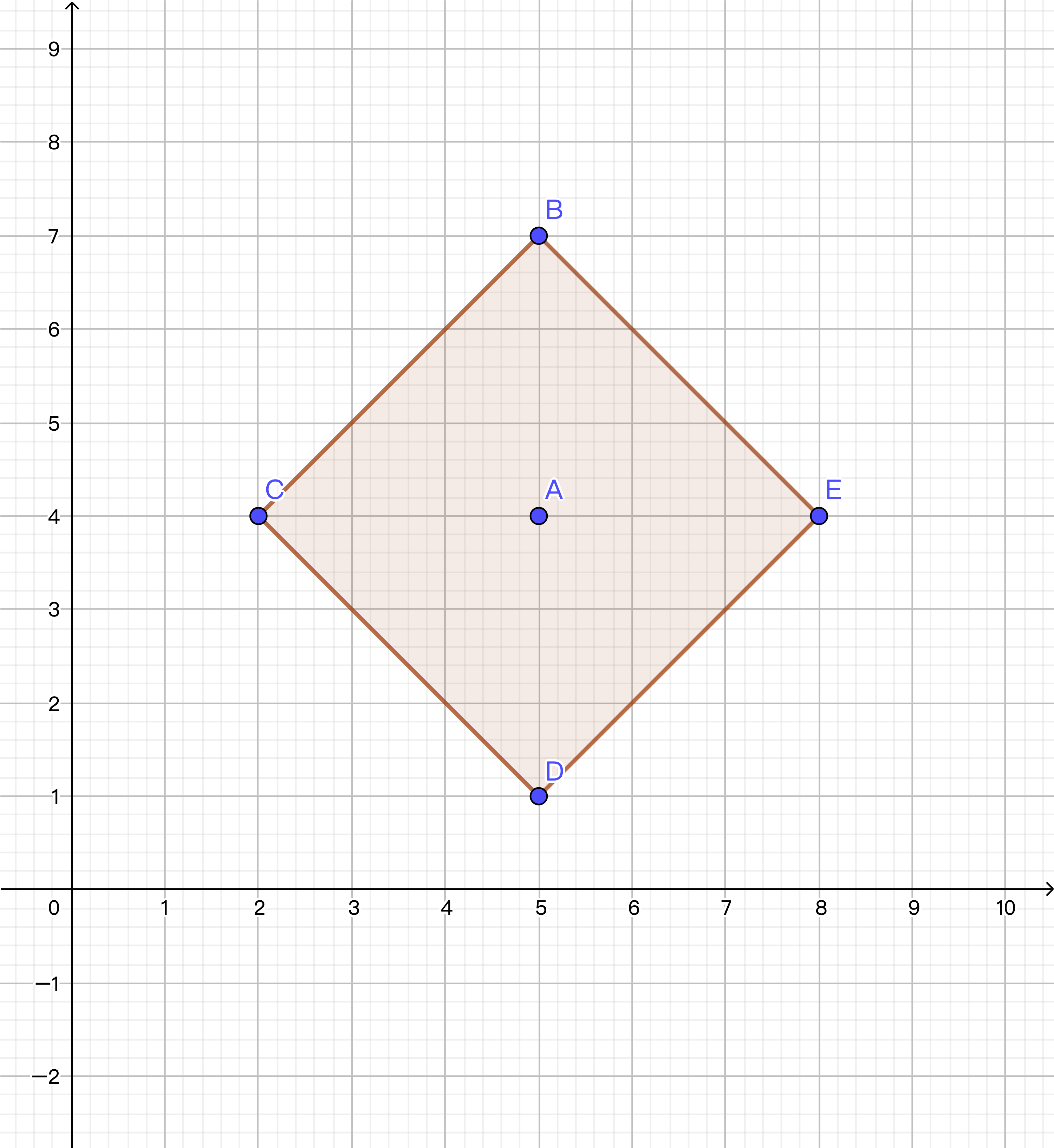
假如一个士兵位于 $A(5,4)$ ，且数值为 $4$。则它的水平、竖直方向与其相差 $\lt 4$ 格的均可被其看到，而根据曼哈顿距离的性质，一个士兵最终的可视范围就是一个正方形，而且这个正方形的对角线长为 $2(x-1)$（以下称 $x$ 为其数值，即范围），而边长为 $\sqrt{2}(x-1)$。

这个可以观测到的点就是在这个正方形内部（包括边和士兵本身），如下图所示的棕色区域：

从特殊到一般

对于任意一个位于 $city_{i,j}$（以下称输入的地图为 $city$）的士兵，它所形成的正方形的四个点分别为 $(\max(1,i-x),j)$、$(i,\max(1,j-x))$、$(\min(n,i+x),j)$ 和 $(i,\min(m,j+x))$。

因为地图上的坐标是正数，所以我们要进行特判，即用 $\max,\min$ 进行修正：

for(int x=max(1,i-d);x<=min(n,i+d);++x)
    for(int y=max(1,j-d);y<=min(m,j+d);++y)
        if(abs(x-i)+abs(y-j)<d)
            flag[x][y]=true;

不妨定义一个 $ans$ 的 $node$ 类型作为答案，使得：

ans=(node){0,0,0x7fffff,0x7fffff,0x7fffff};
// x 和 y 坐标均为 0，步数、隐身和瞬移总使用次数均为 0x7fffff（即 int_max）

如果能到达就进行替换。最后只需判断 $ans.x$ 是否为 $0$ 即可知道是否能到达终点。

在搜索的过程中，我们可将将四种拓展情况进行改动，即：

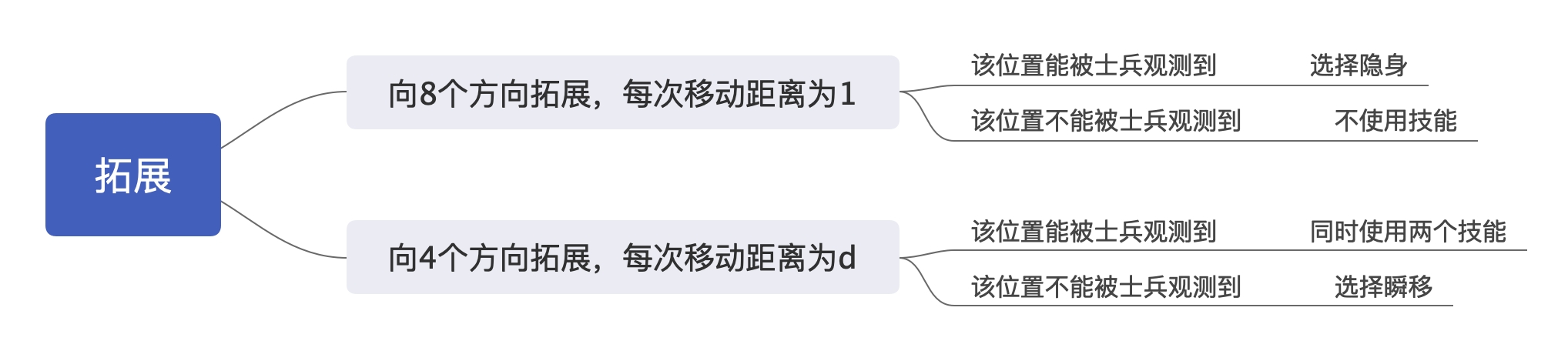
不妨定义一个四维 $visit$ 数组，第一、二下标代表坐标，第三、四坐标分别表示隐身和瞬移的次数。如果重复就不到这个位置——这样能节省时间。

更新答案：

bool check(node a,node b)
{
    if(a.step!=b.step)return a.step<b.step;
    if(a.hide+a.move!=b.hide+b.move)return a.hide+a.move<b.hide+b.move;
    return a.hide<b.hide;
}

把细节注意好了之后（注意：队列数组要开到一千万以上）就能取得 95 分的好成绩（一个点 TLE）。

$100$ 分算法

现在唯一能优化的地方就是士兵观测范围了。这里要用到差分，我们用差分可以有效地解决曼哈顿距离的相关问题。当然下列数组的操作都在新维护的数组 $dif$ 中实现。

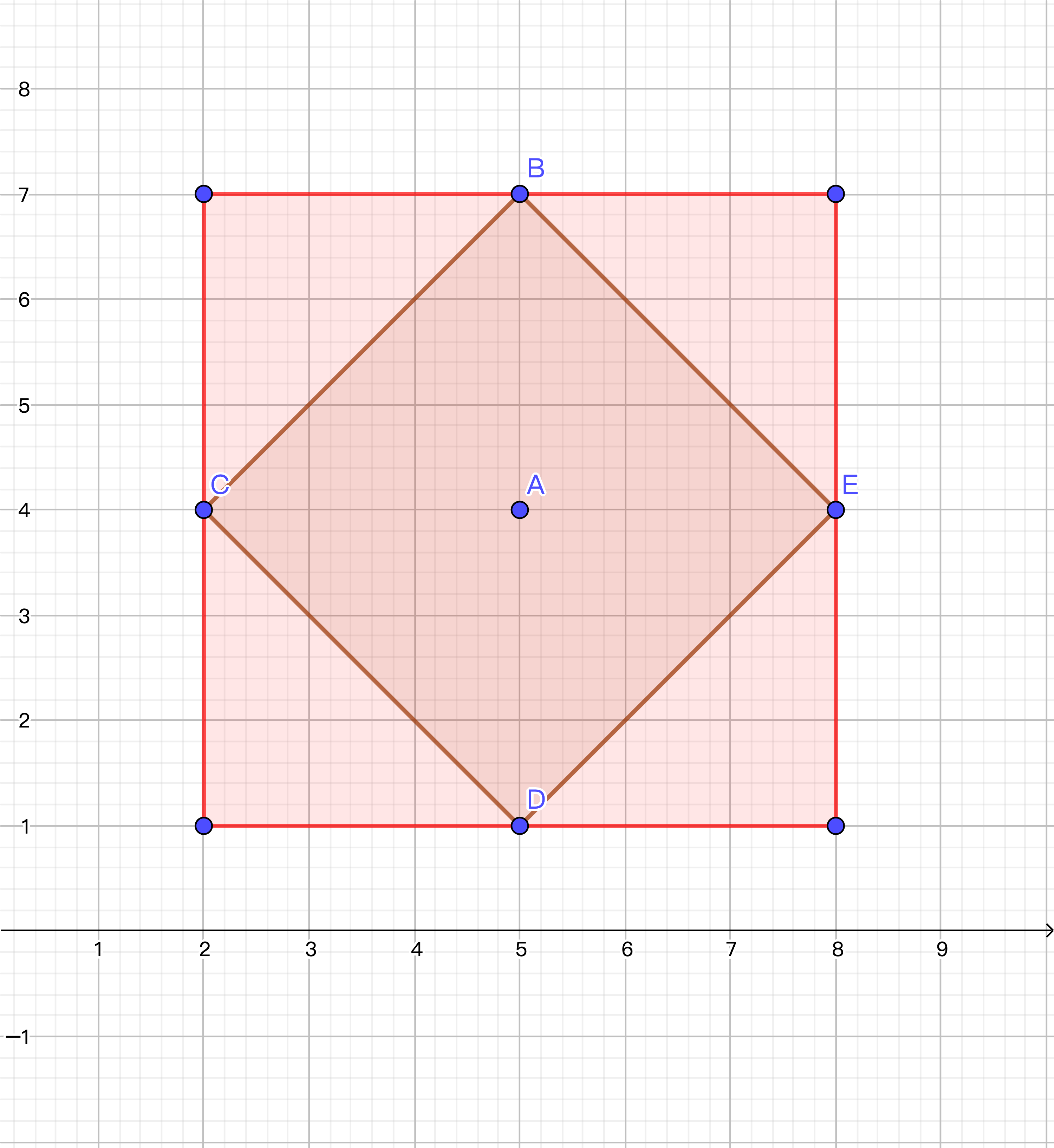
如上图，我们可以在红色正方形内进行操作。曼哈顿距离必定小于 $x$，所以我们不妨进行一个 $i∈[0,x)$ 循环，进行下列操作：

• 上方 $i$ 格，左方 $k-i-1$ 格的位置数值加 $1$

• 上方 $i$ 格，右方 $k-i$ 格的位置数值减 $1$

• 下方 $i$ 格，左方 $k-i-1$ 格的位置数值加 $1$

• 下方 $i$ 格，右方 $k-i$ 格的位置数值减 $1$

这样就能够快速地对周围的格子进行墨水扩散式的遍历，对于每一行，我们不停地求和，然后对于这一行中的每一个元素，如果当前的和大于 $0$，则该格处于观测范围以内：

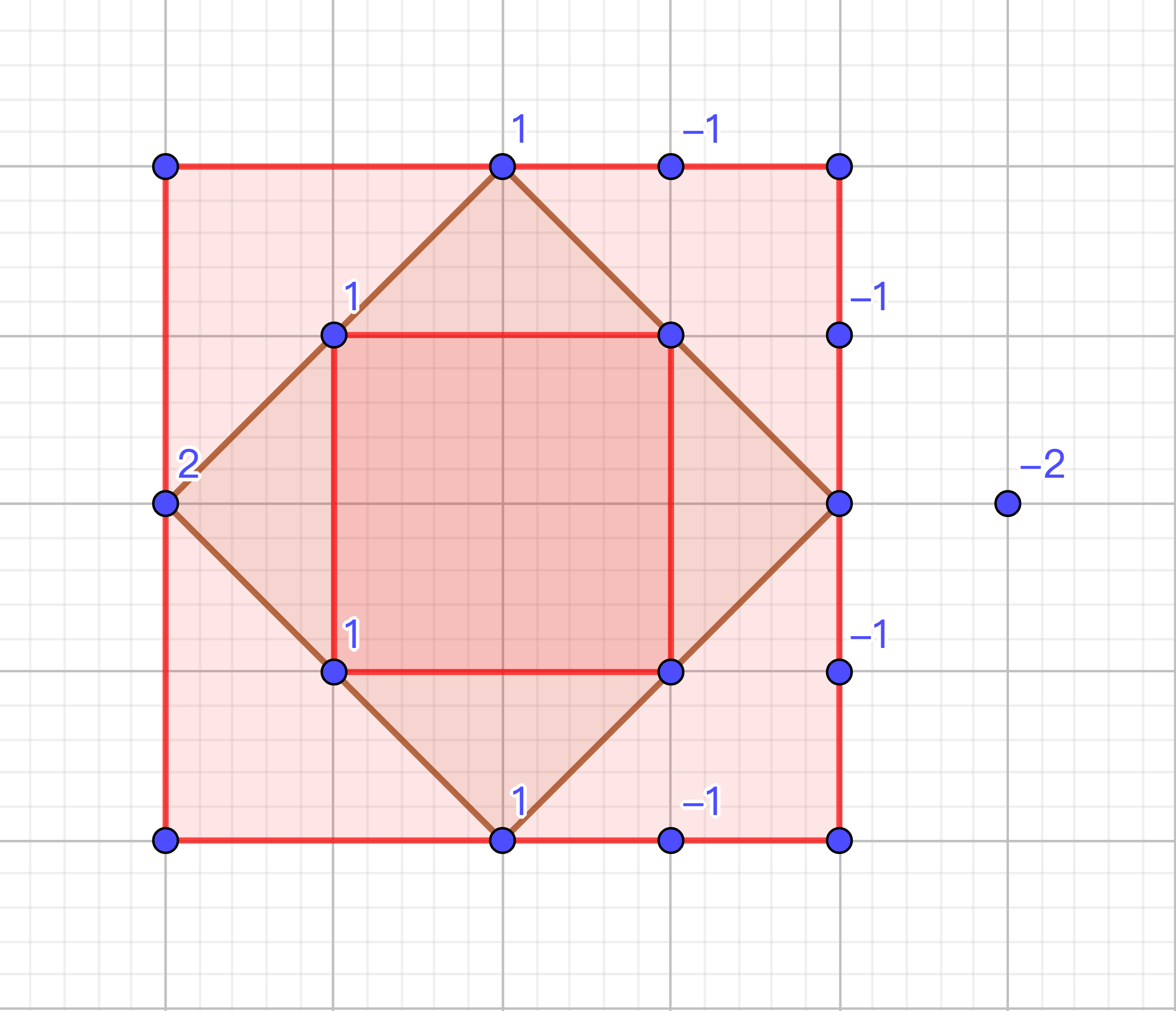
动画演示：

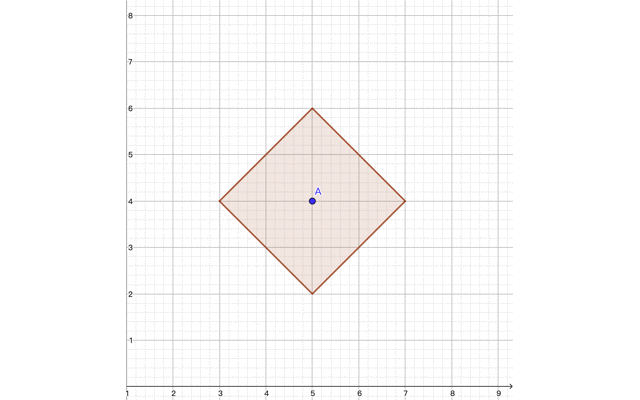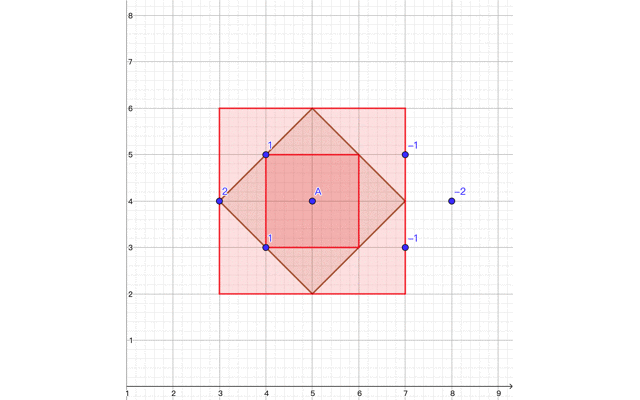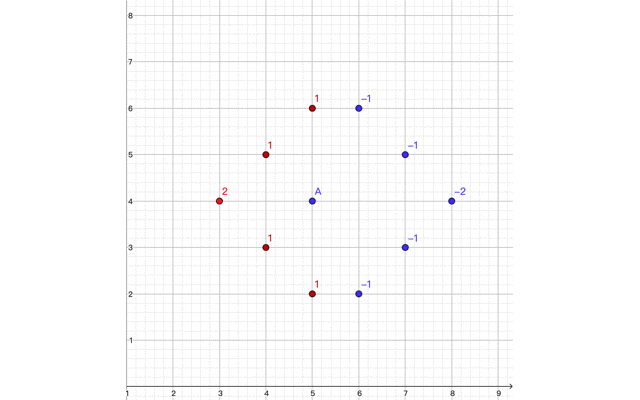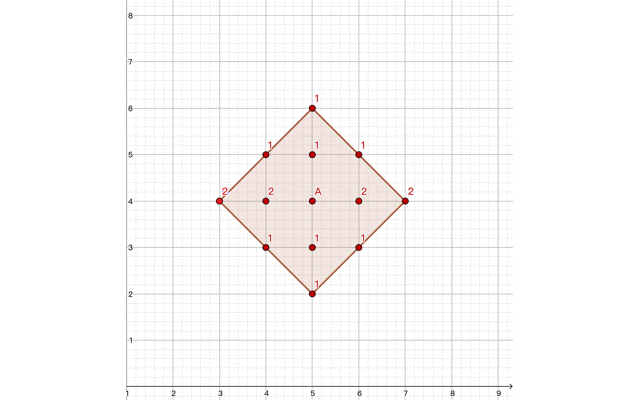
不难发现，可观测到的点恰位于正方形内（包括边）。

实现：

void find(int x,int y,int k)
{
    for(int i=0;i<k;++i)
    {
        ++dif[max(1,x-i)][max(1,y-k+i+1)];
        --dif[max(1,x-i)][min(m,y+k-i-1)+1];
        ++dif[min(n,x+i)][max(1,y-k+i+1)];
        --dif[min(n,x+i)][min(m,y+k-i-1)+1];
    }
}

当然这个差分数组还需使用：

for(int i=1;i<=n;++i) // 对每一行进行操作
{
    int sum=0; // 初始化和
    for(int j=1;j<=m;++j)
    {
        sum+=dif[i][j]; // 累加
        if(sum>0)flag[i][j]=true; // 此时和若大于 0 则标记为真
    }
}

完整代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,c1,c2,d,ex,ey,city[351][351],dif[351][351],dx[]={-1,0,0,1,-1,-1,1,1},dy[]={0,-1,1,0,-1,1,-1,1};
bool flag[351][351],visit[351][351][16][16];
// (ex,ey) 为结束点，city 保存士兵的范围（没有士兵则为 0），dif 为差分维护数组
// flag 为士兵观测数组，visit 为访问数组
struct node
{
    int x,y,step,hide,move;
}q[12500001],ans=(node){0,0,0x7fffffff,0x7fffffff,0x7fffffff};
// q 为队列，ans 为最终答案
void find(int x,int y,int k) // 差分
{
    for(int i=0;i<k;++i)
    {
        ++dif[max(1,x-i)][max(1,y-k+i+1)];
        --dif[max(1,x-i)][min(m,y+k-i-1)+1];
        ++dif[min(n,x+i)][max(1,y-k+i+1)];
        --dif[min(n,x+i)][min(m,y+k-i-1)+1];
    }
}
void input() // 输入
{
    cin>>n>>m>>c1>>c2>>d;
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            string s;
            cin>>s;
            switch(s[0])
            {
                case 'S': // 直接加入队首
                {
                    q[1].x=i;
                    q[1].y=j;
                    break;
                }
                case 'T': // 标记终点
                {
                    ex=i;
                    ey=j;
                    break;
                }
                case '.':break; // 初始化为 0，所以是点的话不需操作
                default:
                {
                    for(int pos=0;s[pos];pos++)city[i][j]=(city[i][j]<<3)+(city[i][j]<<1)+(s[pos]^'0');
                    find(i,j,city[i][j]);
                    // 士兵操作：1、标记，2、差分
                }
            }
        }
    }
}
bool check(node a,node b) // check 函数，判断当前答案是否优于 ans
{
    if(a.step!=b.step)return a.step<b.step;
    if(a.hide+a.move!=b.hide+b.move)return a.hide+a.move<b.hide+b.move;
    return a.hide<b.hide;
}
void bfs()
{
    int front=1,rear=1;
    while(front<=rear)
    {
        node nf=q[front];
        if(nf.step>ans.step) // 此步很重要！有剪枝的效果，可节约大量时间
        {
            front++;
            continue;
        }
        for(int i=0;i<8;++i)
        {
            int nx=nf.x+dx[i],ny=nf.y+dy[i];
            if(nx<1||ny<1||nx>n||ny>m||city[nx][ny])continue; // 判断出边界或已访问
            if(flag[nx][ny]) // 隐身
            {
                if(nf.hide>=c1||visit[nx][ny][nf.hide+1][nf.move])continue;
                visit[nx][ny][nf.hide+1][nf.move]=true;
                q[++rear]=(node){nx,ny,nf.step+1,nf.hide+1,nf.move}; // 入队
                if(nx==ex&&ny==ey&&check(q[rear],ans))ans=q[rear]; // 替换答案
            }
            else // 不用技能
            {
                if(visit[nx][ny][nf.hide][nf.move])continue;
                visit[nx][ny][nf.hide][nf.move]=true;
                q[++rear]=(node){nx,ny,nf.step+1,nf.hide,nf.move};
                if(nx==ex&&ny==ey&&check(q[rear],ans))ans=q[rear];
            }
        }
        for(int i=0;i<4;++i)
        {
            int nx=nf.x+dx[i]*d,ny=nf.y+dy[i]*d;
            if(nx<1||ny<1||nx>n||ny>m||city[nx][ny])continue;
            if(flag[nx][ny]) // 瞬移 + 隐身
            {
                if(nf.hide>=c1||nf.move>=c2||visit[nx][ny][nf.hide+1][nf.move+1])continue;
                visit[nx][ny][nf.hide+1][nf.move+1]=true;
                q[++rear]=(node){nx,ny,nf.step+1,nf.hide+1,nf.move+1};
                if(nx==ex&&ny==ey&&check(q[rear],ans))ans=q[rear];
            }
            else // 瞬移
            {
                if(nf.move>=c2||visit[nx][ny][nf.hide][nf.move+1])continue;
                visit[nx][ny][nf.hide][nf.move+1]=true;
                q[++rear]=(node){nx,ny,nf.step+1,nf.hide,nf.move+1};
                if(nx==ex&&ny==ey&&check(q[rear],ans))ans=q[rear];
            }
        }
        front++; // 队首下标加1
    }
}
int main()
{
    input();
    for(int i=1;i<=n;++i) // 差分
    {
        int sum=0;
        for(int j=1;j<=m;++j)
        {
            sum+=dif[i][j];
            if(sum>0)flag[i][j]=true;
        }
    }
    bfs(); // 搜索
    if(!ans.x)puts("-1"); // 没有答案就输出 -1
    else printf("%d %d %d\n",ans.step,ans.hide,ans.move); // 输出步数、隐身次数和瞬移次数
    return 0;
}