P1928 外星密码 题解

本题有两种方法，一种是纯模拟的思想，一种是递归思想。

$\color{green}{方法}$ $\color{green}{1：字符串处理}$

我们需要操作的对象是方括号内的部分，对于方括号外面的内容，我们不需要进行任何的操作，因此我们要找到最内层的括号，并进行处理。处理完了之后，我们把原来的进行替换。这样一直重复，直到没有括号为止，我们就得到了最终的答案。

例如下面这个数据：

AC[3[3AK]]

上述数据中，最内层的括号组为 [3AK]，而我们可以发现，最内层的左括号是整个字符串最右边的左括号，右括号则是整个字符串最左边的右括号。因此我们只需要写一个循环，找到这两个字符即可。

我们先查找左括号：

int l=-1; // l 保存左括号的位置
for(int i=str.size()-1;i>=0;--i)
{
    if(str[i]=='[')
    {
        l=i;
        break;
    }
}
if(l==-1)break; // 如果找不到，就说明没有括号，即处理完毕

而与之相匹配的右括号必定在左括号的右边，所以搜索范围从 $[0,|str|)$ 变为 $[l,str)$，即：

int r=-1; // r 保存右括号的位置
for(int i=l;str[i];i++) // 搜索区间：从左括号的位置开始到字符串结束
{
    if(str[i]==']')
    {
        r=i;
        break;
    }
}
// 这里不需要特判没有右括号，因为前面在寻找左括号的时候已经特判过了

假如有括号存在，那么被处理的部分则是 $(l,r)$，即两个括号之间（不含括号）的部分。取其子串：

string ns=""; // 初始赋值为空
for(int i=l+1;i<r;i++)ns+=str[i]; // 搜索区间为两括号之间（不含括号），把这一部分内容全部放入 ns 中
str=str.replace(l,r-l+1,rep(ns));

string.replace(start,len,str) 用法：
从 start 这个位置开始，取长度为 len 的字符串，将其替换为 str。

在这个时候，因为区间为 $(l,r)$，即 $[l+1,r-1]$，所以长度为 $r-l+1$。而替换的是这一段处理之后的内容，用一个名为 rep 的函数实现。

接下来我们要完成 rep 函数的实现：

$\color{red}{\text{Step}}$ $\color{red}{0:}$ $\color{red}{初始化}$

将 s 设为函数参数（字符串类型），t 为分离的数字，x 为分离出来的字符串。

$\color{red}{\text{Step}}$ $\color{red}{1:}$ $\color{red}{分离数字}$

我们在整个字符串 s 中处理即可，即区间为 $[0,|s|)$。思路如下：

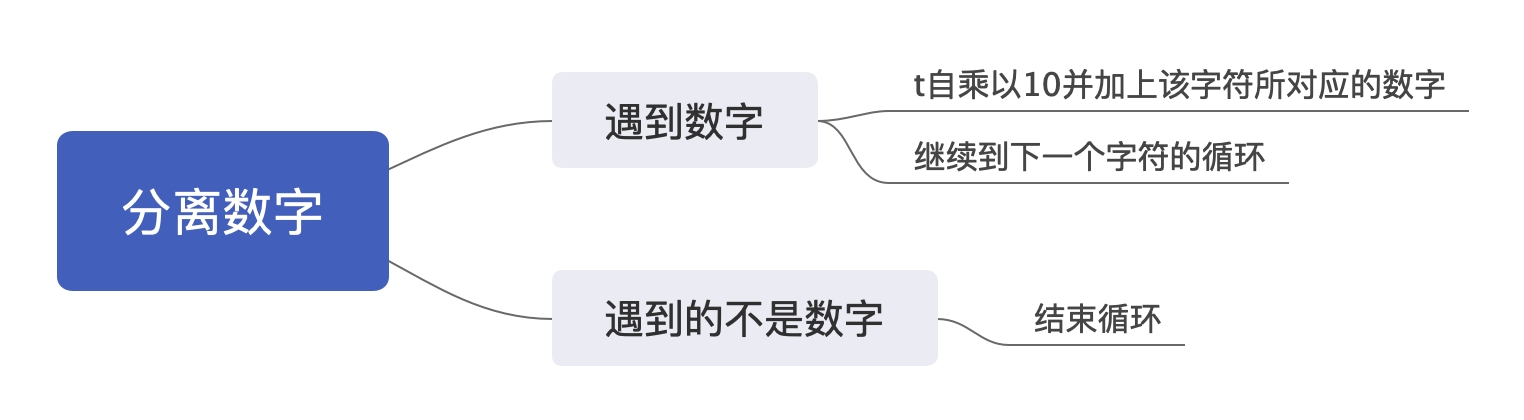
代码：

for(int i=0;s[i];i++)
{
    if(isdigit(s[i]))t=(t<<3)+(t<<1)+(s[i]^48); // t 进行累加
    else break; // 不是数字就跳出循环
}

$\color{red}{\text{Step}}$ $\color{red}{2:} $\color{red}{分离字符串}$

类比分离数字的方法，我们可以用相似的方式处理：

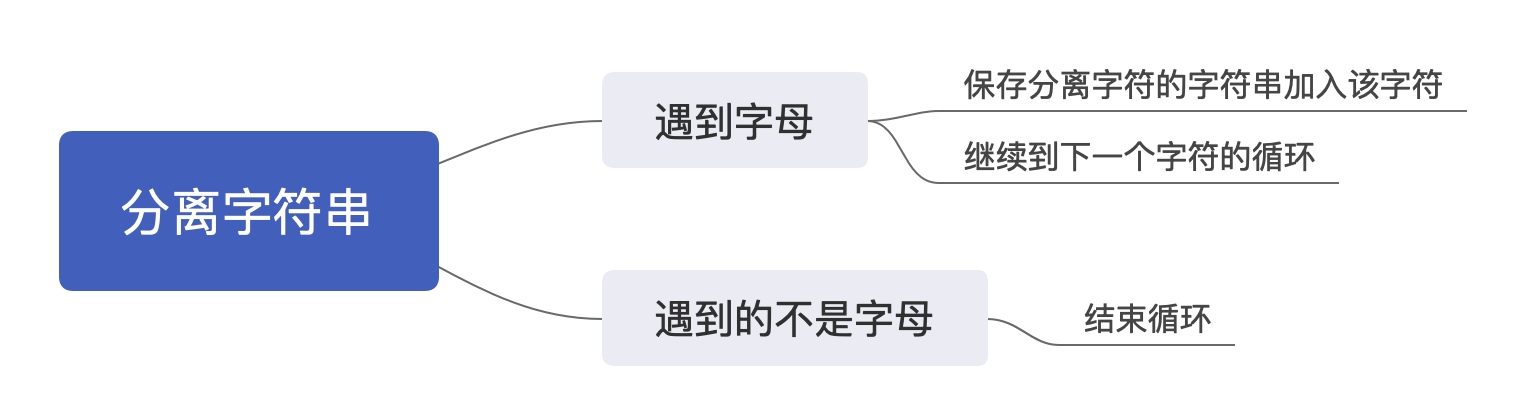
代码：

for(int i=s.size()-1;i>=0;i--)
{
    if(isalpha(s[i]))x+=s[i]; // 字符串加入新字符
    else break; // 退出循环
}
reverse(x.begin(),x.end()); // 注意！我们是倒着进行保存的，所以需要反转

$\color{red}{\text{Step}}$ $\color{red}{3: 拼接}$

新建一个字符串 y，保存拼接的内容，总共包含 t 个 x 字符串。进行拼接：

while(t--)y+=x; // 往 y 中加入 t 个 x
return y; // 返回 y

完整代码：

#include<bits/stdc++.h>
using namespace std;
string str;
string rep(string s)
{
    int t=0;
    for(int i=0;s[i];i++)
    {
        if(isdigit(s[i]))t=(t<<3)+(t<<1)+(s[i]^48);
        else break;
    }
    string x="",y="";
    for(int i=s.size()-1;i>=0;i--)
    {
        if(isalpha(s[i]))x+=s[i];
        else break;
    }
    reverse(x.begin(),x.end());
    while(t--)y+=x;
    return y;
}
int main()
{
    cin>>str;
    while(true)
    {
        int l=-1,r=-1;
        for(int i=str.size()-1;i>=0;i--)
        {
            if(str[i]=='[')
            {
                l=i;
                break;
            }
        }
        if(l==-1)break;
        for(int i=l;str[i];i++)
        {
            if(str[i]==']')
            {
                r=i;
                break;
            }
        }
        string ns="";
        for(int i=l+1;i<r;i++)ns+=str[i];
        str=str.replace(l,r-l+1,rep(ns));
    }
    cout<<str;
    return 0;
}

$\color{green}{方法}$ $\color{green}{2：递归}$

本题同样可以使用递归的算法：

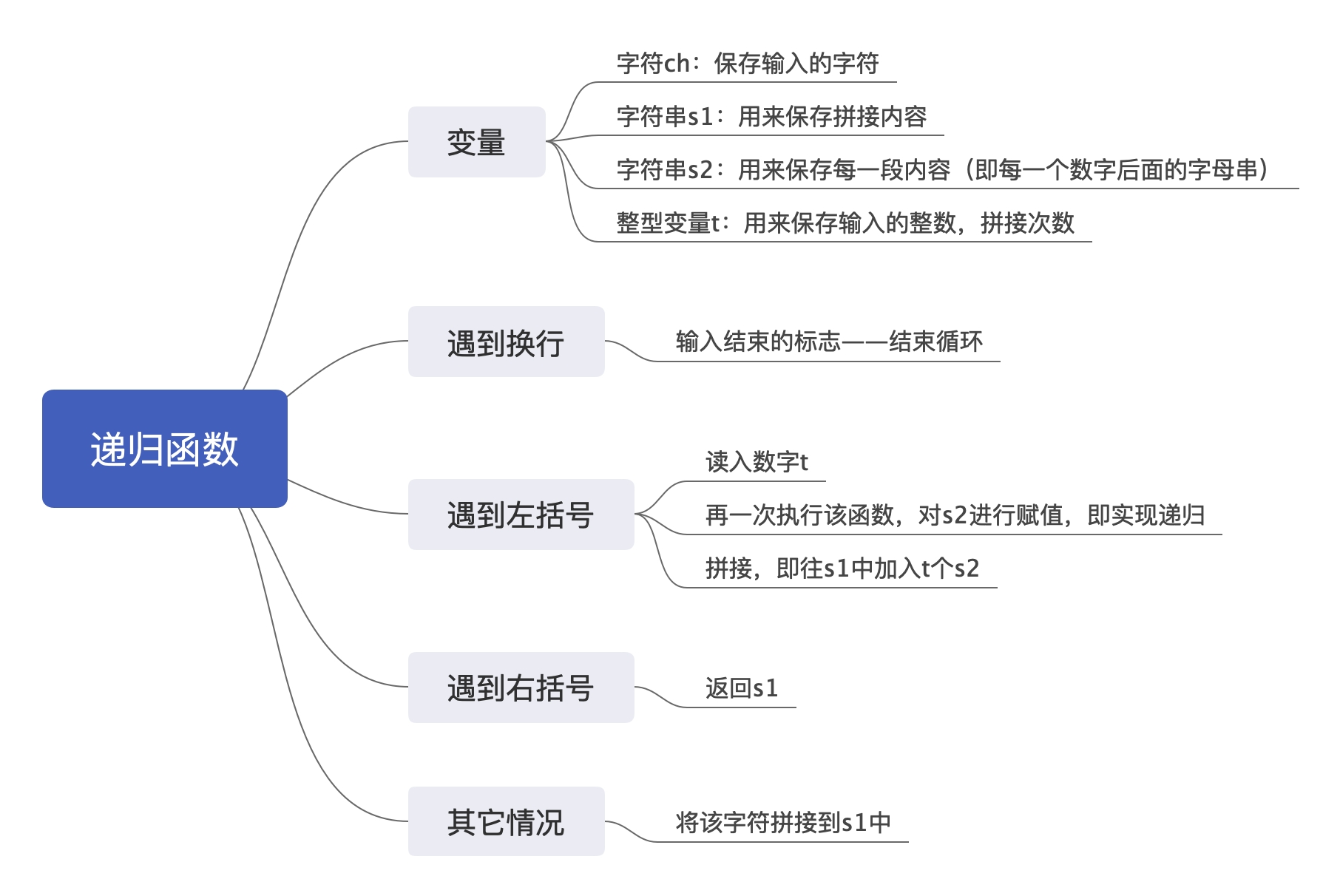
主函数只需调用递归函数即可，因为递归函数既实现输入，又实现了字符串的处理。

完整代码：

#include<bits/stdc++.h>
using namespace std;
string f()
{
    string s1="",s2;
    char ch;
    while(cin>>ch)
    {
        if(ch=='\n')break;
        if(ch=='[')
        {
            int t;
            scanf("%d",&t);
            s2=f();
            while(t--)s1+=s2; 
        }
        else if(ch==']')return s1;
        else s1+=ch;
    }
}
int main()
{
    cout<<f();
    return 0;
}