P11362 [NOIP2024] 遗失的赋值 题解

首先，需要特判 $c_i = c_j$ 但 $d_i \neq d_j$ 的情形，此时答案为 $0$。

否则，我们可以把每相邻的两条一元限制作为一个区间单独拎出来。这样做正确的原因是，每一个 $x_i$ 的取值只受前面一个数的影响。事实上，完全可以任意选取区间，只不过这样选可以利用已知的 $x_i$，依次讨论出 $a_{i+1}, b_{i+1}, a_{i+2}, b_{i+2}, \cdots$ 的可能取值，便于计算答案。

我们随便找几个数举个例子：

此时分别考虑区间 $[2,6]$，$[6,7]$ 和 $[7,9]$ 即可。

---

对于相邻的两条一元限制 $(c_i, d_i)$，$(c_j, d_j)$（$c_i \lt c_j$）：

区间 $[c_i,c_j]$ 内有 $c_j - c_i$ 条待定的二元限制。

由于要求的是至少存在一种合法的 $x_i$ 的赋值方案数，我们不妨考虑其反面，先找出所有的方案，使得不存在合法的 $x_i$ 的赋值方式。

---

先考虑最特殊的一种情形，即从 $c_i$ 位置开始，首先有 $a_{c_i} = d_i$，而后有 $b_{k-1} = a_k$（$c_i \lt k \lt c_j$）。换言之，这种构造可以使得从 $c_{i} + 1$ 位置到 $c_{j} - 1$ 位置的 $x$ 值都确定下来。既然想要使方案不合法，我们只需进一步使 $b_{c_j-1} \neq d_j$ 即可。

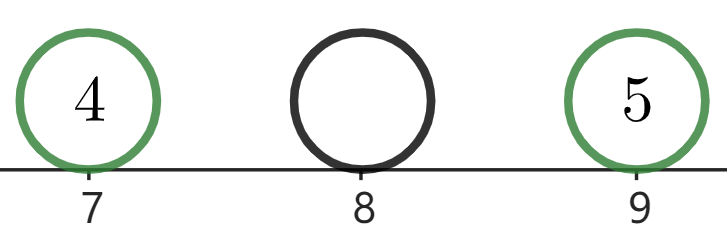
例如，对于 $[2,6]$ 这个区间，一种不合法的方案是：

• 令 $a_2 = 1$，$b_2 = 3$，则 $x_3$ 被确定为 $3$。
• 令 $a_3 = 3$，$b_3 = 2$，则 $x_4$ 被确定为 $2$。
• 令 $a_4 = 2$，$b_4 = 3$，则 $x_5$ 被确定为 $3$。
• 令 $a_5 = 3$，$b_5 = 2$，则 $x_6$ 被确定为 $2$。

但从初始情况可知 $x_6$ 已经为 $1$，因此这种方案不合法。

---

从 $c_i$ 位置到 $c_j-2$ 位置，$b_k$ 可以在 $1 \sim v$ 内任取，而 $b_{c_j-1}$ 又有 $v-1$ 种取法（因为要保证不与 $d_j$ 相同）。则在这种情形下不合法的方案数为 $\color{red}{v^{c_j-c_i-1}(v-1)}$。

例如，对于上面的例子，若 $v = 5$，那么首先 $a_2$ 必须为 $1$，而 $b_2$ 可以取 $1 \sim 5$ 内的任意一个值。进一步地：

• $a_3 = b_2$，但 $b_3$ 可在 $1 \sim 5$ 内任取。
• $a_4 = b_3$，但 $b_4$ 可在 $1 \sim 5$ 内任取。
• $a_5 = b_4$，由于要保证 $b_5 \neq d_6$，因此 $b_5$ 可以取 $2 \sim 5$ 内的任意一个值。

因此不合法的方案数为 $5^3 \times 4 = 500$。

---

否则，区间内存在一个位置 $k$ （$c_i \lt k \lt c_j$）使得 $b_{k-1} \neq a_k$。那么我们只需要让 $x_k$ 取任意一个不等于 $a_k$ 的数，就能使 $x_{k+1}$ 的取值不受约束。依此类推，后面的数都可以任意选取，因此一定存在至少一种符合题意的 $x_i$ 的构造方案。即这种情形下的方案均合法。

例如，对于 $[7,9]$ 这个区间，我们可以让 $a_7 = 4$，$b_7 = 5$，但 $a_8 = 3 \neq b_7$（即 $a_8 \neq x_8$）。这时，无论 $b_8$ 取何值，$x_9$ 的值都将不受约束。

---

当不考虑一元限制时，每个 $a_k$，$b_k$ 都各能在 $1 \sim v$ 内任取，因此总方案数为 $\color{red}{v^{2(c_j-c_i)}}$。

因此，对相邻的两条一元限制 $(c_i, d_i)$，$(c_j, d_j)$（$c_i \lt c_j$），用总方案数减去不合法的方案数，即为合法的方案数：$\color{red}{v^{2(c_j-c_i)} - v^{c_j-c_i-1}(v-1)}$。

---

当然，还需处理边界，每个 $a_k$，$b_k$ 都各能在 $1 \sim v$ 内任取，因为我们总可以对应地构造出符合的 $x_k$，理由同上。

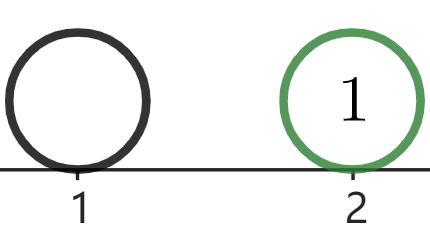
例如，对于 $[1,2]$ 这个区间，若 $v = 5$，$a_1$ 和 $b_1$ 都各能在 $1 \sim 5$ 内的任取，因为只需使 $x_1 \neq a_1$ 即可。

---

在代码实现上，可以对原 $(c_i, d_i)$ 序列进行排序、去重（或者直接用 map，通过迭代器来遍历），然后用快速幂计算即可。

• 时间复杂度：$O(m(\log m + \log n)) \approx O(m \log n)$。
• 空间复杂度：$O(m)$。

#include <bits/stdc++.h>
using namespace std;
const int p = 1000000007;
int T, n, m, v;
struct node {
    int c, d;
    bool operator<(const node &x) const {
        if (c != x.c) return c < x.c;
        return d < x.d;
    }
    bool operator==(const node &x) const {
        return c == x.c && d == x.d;
    }
} con[100001];
long long qpow(long long a, long long b) {
    long long s = 1;
    while (b) {
        if (b % 2 == 1) s = s * a % p;
        a = a * a % p;
        b /= 2;
    }
    return s;
}
namespace IO {
    char buf[1 << 21], *p1 = buf, *p2 = buf, obuf[1 << 21], *p3 = obuf;
    char gc() {
        if (p1 == p2) {
            p1 = buf;
            p2 = buf + fread(buf, 1, 1 << 21, stdin);
        }
        return p1 == p2 ? EOF : *p1++;
    }
    template<typename T> void read(T &x) {
        x = 0;
        char ch = gc();
        while (!isdigit(ch)) ch = gc();
        while (isdigit(ch)) {
            x = (x << 3) + (x << 1) + (ch ^ 48);
            ch = gc();
        }
    }
    void pc(char c) {
        if (p3 - obuf < (1 << 21)) *p3++ = c;
        else {
            fwrite(obuf, p3 - obuf, 1, stdout);
            p3 = obuf;
            *p3++ = c;
        }
    }
    template<typename T> void write(T x) {
        if (x > 9) write(x / 10);
        pc(x % 10 + 48);
    }
} using namespace IO;
int main() {
    #ifndef ONLINE_JUDGE
        freopen("assign.in", "r", stdin);
        freopen("assign.out", "w", stdout);
    #endif
    read(T);
    while (T--) {
        read(n), read(m), read(v);
        long long ans = 1;
        for (int i = 1; i <= m; i++) read(con[i].c), read(con[i].d);
        sort(con + 1, con + m + 1);
        for (int i = 1; i <= m; i++) {
            if (con[i].c == con[i-1].c && con[i].d != con[i-1].d) {
                ans = 0;
                break;
            }
        }
        if (ans != 0) {
            m = unique(con + 1, con + m + 1) - con - 1;
            ans = ans * qpow(v, 2 * (con[1].c - 1));
            for (int i = 2; i <= m; i++) {
                int d = con[i].c - con[i-1].c;
                long long cur = (qpow(v, 2 * d) + p - (1LL * (v - 1) * qpow(v, d - 1) % p)) % p;
                ans = ans * cur % p;
            }
            ans = ans * qpow(v, 2 * (n - con[m].c)) % p;
        }
        write(ans);
        pc('\n');
    }
    fwrite(obuf, p3 - obuf, 1, stdout);
    return 0;
}